This is probably one of the most important articles for long-term success in trading that I have written so far. If I am not mistaken, this is the first time I have written about it, although the issue of risk of ruin is of the utmost importance in achieving long-term profitability. It is about evaluating, objectively, the risk I have of losing a certain percentage of the capital dedicated to investment and trading.
We have talked a lot in the past about drawdowns in general and in trading systems in particular. Specifically, we have explained the concept of the historical maximum drawdown as a risk measure of any kind.
When using a trading system in Forex and in other markets we must be able to answer two questions:
- With a certain capital, what risk do I have of suffering catastrophic losses in the system/portfolio due to lack of funds?
- If I want to risk only a certain capital, what probability of success do I have in the long term?
They are two questions that come to express the same thing, the relationship between the probability of long-term success and the capital available for the system/portfolio. Naturally we all know that the more we put in, the better, but it is about optimizing the use of money, right?
The answer to all these questions (and many more) is found in the book The Theory of Stochastic Processes (Science Paperbacks) written before I was born (but not much by the way). Don’t buy it, save it. It is a dense book on statistics with many formulas and Greek letters.
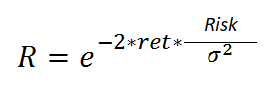
In the book there is a formula that establishes the relationship between the monthly return (it can be from another period as well) of the strategy, the standard deviation of said return, the percentage of the balance that you want to risk and the probability of the event occurring ( that capital is lost). I will spare you the explanations of the reason for the validity of the formula, but believe me that it is totally applicable. Don’t panic, I’m not going to go into more details, so let’s get to the point.
Suffice it to know that R is the probability that you will lose a certain percentage of capital (risk) given a return (ret) and a standard deviation of that return (s2). In this way, knowing those three data, I can calculate the probability that I will lose that amount of capital. Let’s see a real example:
I recently made a selection of 4 forex systems that I understand make up a good strategy for 2020. Let’s see what happens if we use the numbers from that portfolio with this formula. The results for the proposed starting capital ($25,000) are:
- Average monthly return: $2480
- Standard deviation of average monthly return: $3123
The Margin Call risk curve (running out of money to have enough collateral to support positions) would come out as follows:
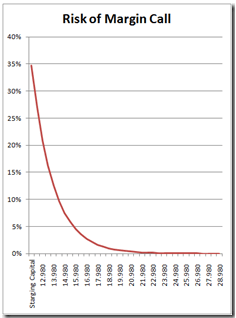
As can be seen, to have a risk of less than 5% of losing our trading capital we should have something more than $16,500 in our account. With a capital of $25,000 we would have an almost negligible risk of 0.1%.
This, which seems like magic or a non-applicable theory, is not. The trick is in the relationship between the average profit (in this case monthly) and the standard deviation of it. That is, in the homogeneity of earnings. The less homogeneous the earnings, the worse the curve develops and the easier it is to lose the trading account. If we increase the standard deviation to $4000, for example (the increase would have been approximately 30%), the probability of a total loss would be multiplied by 10 (although it would still be very low at 1.1%). Note that we DO NOT TOUCH the average monthly return, that is, the portfolio of strategies continues to earn the same, but does so with greater volatility.
Now, we could use this powerful formula to do the reverse. I want to know how likely I am to lose my trading account (risk of ruin) if I only want to risk a certain amount of capital. It is really very simple because it would consist of analyzing the chart along the axis below and considering the margin that the broker demands.
Let’s see an example below:
In this strategy portfolio the margin demanded by the Forex broker is $10,400. Let’s imagine that I don’t want to risk more than $5000 of my money to trade this series of trading systems. The beginning balance will then be $15,400. The risk obtained from the graph is slightly less than 8%, which can be appreciated by zooming in on the previous graph:

In other words, if we wanted to trade with this portfolio by risking only $5,000, we would have a 92% probability of success. In other words, 92 out of 100 times that we start trading with this portfolio with $15,400, we will end up making money while the other 8 times we will lose the money in our account because we have chosen the wrong time to enter.
As you can see, this is a relatively simple way to calculate my risk of ruin given some parameters that we understand and, even better, we can control. Obviously it will always be better to invest as much capital as possible, but that does not have to be optimal. In this portfolio, for example, a capital above $25,000 already forces me to have to look for the second decimal to see the risk of ruin, so it would be a waste of time.